Poj3684题解 Physics Experiment 弹性碰撞

题意

看上去像是很普通的高中物理题目，下落方式有两个要点:初始时所有小球挤在一起放置和每隔一秒钟扔一个小球

笺释

我觉得这个题并不像大多数人说的那么轻松，可能是我理解水平和智力水平都低于他们吧，~~总之我觉得这道题并不是一句简简单单的和蚂蚁那道题差不多就能搞定的。~~

第一个要点是

先放置的小球永远先处于所有小球的下面，所以这道题如果明确要求说要按照一开始扔小球的顺序来输出答案，其实和直接输出答案是同样的结果。

第二个要点来自于弹性碰撞

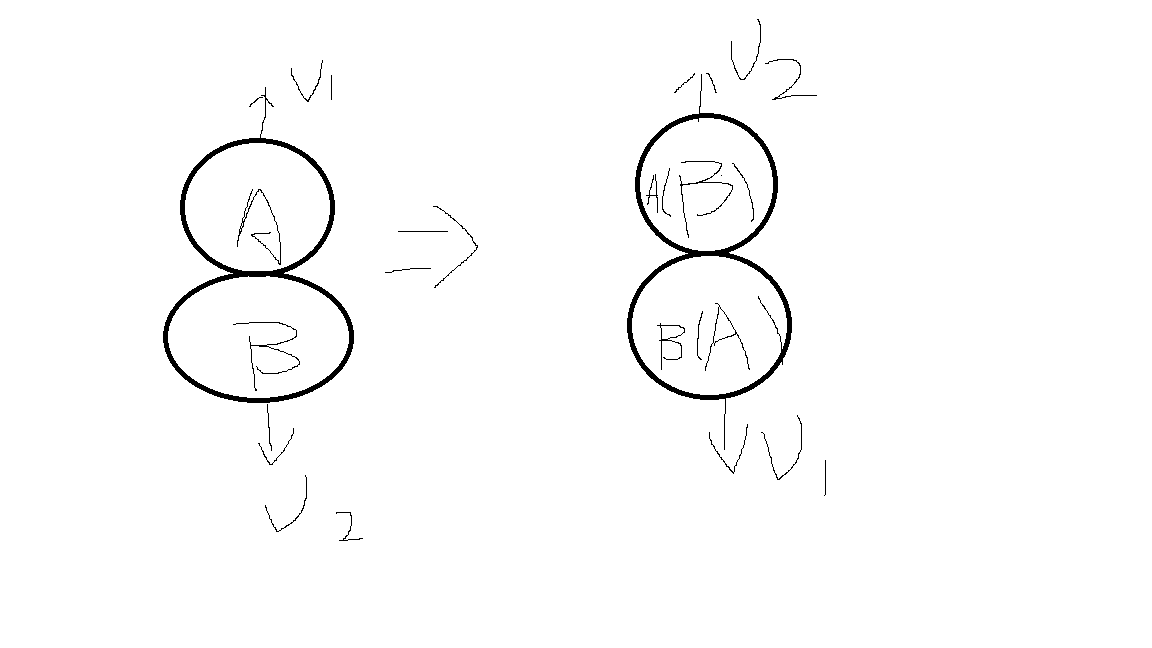
因为是弹性碰撞，所以小球A和小球B发生弹性碰撞之后相当于小球B向上瞬移了2r之后以之前的速度继续向上，小球A向下瞬移了2r之后以之前的速度继续向下。注意弹性碰撞是交换速度而不是自身速度反向。但是这一点相当于能推出什么样的结论呢?从最严格的角度来说，我觉得这只是提供了一种模拟的思路，我们可以通过这个要点简化模拟，但是更多的要点至少从这个角度来说我是比较难直接给出很好的诠释的。

第三个要点要求必须把r视为0

现在对第二个要点进行加强，在第二个要点中，如果r为0，小球A和小球B发生弹性碰撞之后相当于小球B向上瞬移了2r(0)之后以之前的速度继续向上，小球A向下瞬移了2r(0)之后以之前的速度继续向下，而通过这一点，我们就可以说，最终状态的位置和只是计算单个小球与地面碰撞而不考虑小球之间的碰撞所产生的位置是一一对应的关系。

而这个结论还要经过这样的说明

考虑进去小球之间的碰撞之后进行模拟所得到的最终位置有n个，不考虑碰撞之后进行计算所得到的最终位置有n个，因为碰撞本身对位置本身是没有产生改变的，我们不考虑小球交换了还是怎么样，仅仅从位置的角度考虑，每一个位置之间是完全的对应，而由于要点1，我们能够确定小球的位置。

第四个要点要求把每一个小球看作是一个虚像小球被另一个小球拉着。

现实情况r并不是0，又该怎么考虑呢?

看作每一个有半径的小球对应一个没有半径的小球，每一个没有半径的小球(质点)拉着那个有半径的小球运动，因为没有r，所以小球一开始是放在一起的(质点是重叠在一起的)，而每个质点拉着一个距离其2（i-1)r的小球，小球的位置永远处于这个质点的上方2（i-1)r处。

综上所述

完整代码

#include
    
     #include 
     
      #include 
      
       #include 
       
        #include 
        
         #include 
         
          #include 
          
           #include 
           
            #include
            #include 
             
              #include 
              
               using namespace std;#define MM(a) memset(a,0,sizeof(a))typedef long long LL;typedef unsigned long long ULL;const int mod = 1000000007;const double eps = 1e-10;const int inf = 0x3f3f3f3f;const double g=10;int cas,n,r,t,k;double h;double t0,tx,a[105],temp;double solve(int x){ if(x<0) return h; t0=sqrt(2*h*1.0/g); k=int(x/t0); if(k%2==0) temp=x-k*t0; else temp=t0-(x-k*t0); //cout<
               
                <
                
                 >cas; while(cas--) { scanf("%d %lf %d %d",&n,&h,&r,&t); for(int i=1;i<=n;i++) { a[i]=solve(t-(i-1)); } sort(a+1,a+n+1); for(int i=1;i<=n;i++) printf("%.2f%c",a[i]+2.0*(i-1)*r/100.0,i==n?'\n':' '); } return 0;}

感谢

转载于:https://www.cnblogs.com/SoniciSika/p/9034202.html

你可能感兴趣的文章